¿Cuál es la mejor manera de establecer las casas para una carta armónica? Esta es una cuestión particular que afecta al trabajo astrológico con armónicos, por lo que suponemos que el lector tiene ya algún conocimiento de Teoría Armónica. Si no es así, tómese unos minutos para leer, al menos, el trabajo de Dumon Armónicas en Astrología.
El problema de la domificación de las cartas armónicas
Las cartas armónicas son variaciones de la carta radical, o más bien extensiones de la misma, que se obtienen multiplicando por algún número entero las longitudes eclípticas de todos y cada uno de sus puntos. Si el resultado de alguna de las operaciones excede de 360º, hay que restar esta cantidad tantas veces como sea necesario para acotar la posición armónica dentro de los límites normales del zodiaco. En cada carta armónica, el número entero que se utiliza es el mismo para todos los puntos, y sirve para identificar esa carta. Así, por ejemplo, si multiplicamos por 2 las longitudes eclípticas de todos los puntos de una carta y dibujamos en una carta nueva el resultado de estas operaciones, la carta resultante se denominará armónico 2.
Tomemos, por ejemplo, la carta radical del propio John Addey, el gran impulsor de la teoría armónica en occidente, nacido el 15 de junio de 1920, 7h 15m GMT, en Barnsley, 1º 28' W, 53º 34' N.
Si tratamos de calcular el armónico 2 de esta carta, o de cualquier otra, enseguida nos daremos cuenta de que se nos plantea una dificultad tan pronto como queramos representarla gráficamente. La dificultad es aún mayor si nos obstinamos en mantener a toda costa la misma apariencia general que tiene normalmente cualquier carta radical. En casi todos los sistemas de casas, las cúspides se oponen dos a dos. El Ascendente queda en exacta oposición al Descendente, el Medio Cielo en exacta oposición al Fondo Cielo, y así con todas las demás cúspides. Pero es una norma general de la matemática armónica que dos puntos cualesquiera de una carta radical que estén en oposición exacta, formarán una conjunción exacta en el armónico 2 y en todos sus múltiplos. La consecuencia natural de esta norma es que, en el armónico 2, hacen conjunción todos los pares de cúspides opuestas: el Ascendente queda en el mismo lugar que el Descendente, el Medio Cielo en el mismo lugar que el Fondo Cielo, etc.
A medida que ascendemos por la escala de los números enteros, las cartas armónicas asociadas presentan distribuciones cada vez más aberrantes de las cúspides de las casas, que pueden aparecer a cualquier distancia unas de otras y en cualquier orden. De modo que, a estas alturas, carece completamente de sentido pretender que el espacio comprendido entre dos cúspides de casas de numeración consecutiva en una carta armónica defina adecuadamente el tamaño y los límites de esa casa.
A este problema se han dado, básicamente, tres soluciones, ninguna de las cuales es del todo satisfactoria. Para empezar por la más extendida, -que, dicho sea de paso, es, bajo mi punto de vista, la menos acertada de las tres- se calcula la nueva posición del Ascendente en el armónico de que se trate, y, a partir de ahí, se aplica un sistema de casas iguales, añadiendo una cúspide de casa cada 30 grados. Obviamente, lo que así se obtiene son once cúspides intrusas, que nada tienen que ver con el armónico en cuestión. A lo sumo, se les puede conceder a esas cúspides el débil valor de representar lugares de aspecto al Ascendente armónico. Pero este privilegio tienen igual derecho a reclamarlo todas las demás cúspides, planetas o puntos calculados. Por otra parte, lo más interesante de una carta armónica son sus conjunciones, porque los demás aspectos remiten a otros armónicos más altos. Se obtiene así, desde luego, la hermosa apariencia de una carta radical, pero sólo a costa de decorados de cartón piedra que no pertenen al paisaje natural de la carta armónica.
Figura 3. John Addey. Armónico 2. Cúspides armónicas en sus verdaderos lugares
Tomemos, por ejemplo, la carta radical del propio John Addey, el gran impulsor de la teoría armónica en occidente, nacido el 15 de junio de 1920, 7h 15m GMT, en Barnsley, 1º 28' W, 53º 34' N.
Figura 1. John Addey. Armónico 1
A medida que ascendemos por la escala de los números enteros, las cartas armónicas asociadas presentan distribuciones cada vez más aberrantes de las cúspides de las casas, que pueden aparecer a cualquier distancia unas de otras y en cualquier orden. De modo que, a estas alturas, carece completamente de sentido pretender que el espacio comprendido entre dos cúspides de casas de numeración consecutiva en una carta armónica defina adecuadamente el tamaño y los límites de esa casa.
A este problema se han dado, básicamente, tres soluciones, ninguna de las cuales es del todo satisfactoria. Para empezar por la más extendida, -que, dicho sea de paso, es, bajo mi punto de vista, la menos acertada de las tres- se calcula la nueva posición del Ascendente en el armónico de que se trate, y, a partir de ahí, se aplica un sistema de casas iguales, añadiendo una cúspide de casa cada 30 grados. Obviamente, lo que así se obtiene son once cúspides intrusas, que nada tienen que ver con el armónico en cuestión. A lo sumo, se les puede conceder a esas cúspides el débil valor de representar lugares de aspecto al Ascendente armónico. Pero este privilegio tienen igual derecho a reclamarlo todas las demás cúspides, planetas o puntos calculados. Por otra parte, lo más interesante de una carta armónica son sus conjunciones, porque los demás aspectos remiten a otros armónicos más altos. Se obtiene así, desde luego, la hermosa apariencia de una carta radical, pero sólo a costa de decorados de cartón piedra que no pertenen al paisaje natural de la carta armónica.
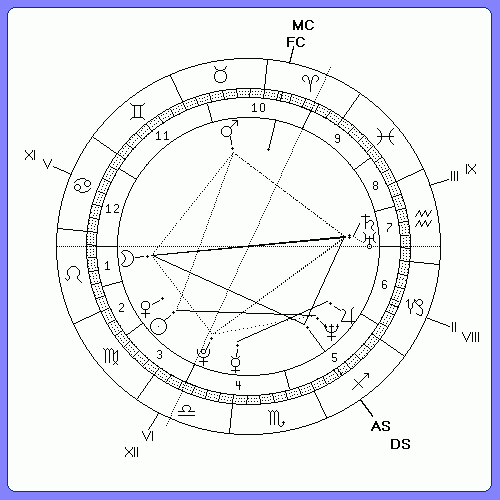
Figura 2. John Addey. Armónico 2.
Casas iguales (no armónicas) añadidas a partir del Ascendente armónico
La segunda solución, matemáticamente irreprochable, consiste en dibujar cada cúspide en cualquier sitio que caiga en el zodiaco de la carta armónica, despreocupándonos por completo de los límites de las casas y atendiendo únicamente a los aspectos, tanto de los planetas entre sí, como de estos con las cúspides y hasta de las cúspides entre sí. De esta forma, las casas pierden su carácter sectorial, quedando confinadas a puntos (sus cúspides) que las representan en su totalidad. Esta solución exige nuevos hábitos de interpretación, que hasta ahora nadie ha definido, y sólo mantiene la coherencia del cálculo a costa de una representación final de apariencia caótica.
| Cúspides | John Addey | |||
| Armónico 1 | Armónico 2 | |||
| I | 125º 43' 31" | 5º 44' Leo | 251º 27' 02" | 11º 27' Sag |
| II | 141º 38' 19" | 21º 38' Leo | 283º 16' 38" | 13º 17' Cap |
| III | 162º 20º 03' | 12º 20' Vir | 324º 40' 06" | 24º 40' Acu |
| IV | 191º 28' 34" | 11º 29' Lib | 22º 57' 08" | 22º 57' Ari |
| V | 231º 48' 09" | 21º 48' Esc | 103º 36' 18" | 13º 36' Cán |
| VI | 274º 05' 33" | 4º 06' Cap | 188º 11' 06" | 8º 11' Lib |
| VII | 305º 43' 31" | 5º 44' Acu | 251º 27' 02" | 11º 27' Sag |
| VIII | 321º 38' 19" | 21º 38' Acu | 283º 16' 38" | 13º 17' Cap |
| IX | 342º 20º 03' | 12º 20' Pis | 324º 40' 06" | 24º 40' Acu |
| X | 11º 28' 34" | 11º 29' Ari | 22º 57' 08" | 22º 57' Ari |
| XI | 51º 48' 09" | 21º 48' Tau | 103º 36' 18" | 13º 36' Cán |
| XII | 94º 05' 33" | 4º 06' Cán | 188º 11' 06" | 8º 11' Lib |
La tercera solución, aparentemente la más cómoda, hasta el punto de que parece más una huida del problema que una verdadera solución, consiste en mantener intactas las cúspides radicales del armónico 1. Sin embargo hay, al menos, dos buenas razones para esta opción. La primera es que las transformaciones armónicas en rigor sólo afectan al zodíaco, no a las casas. La segunda es de tipo empírico y se basa en las posibilidades que ofrecen las cartas armónicas como sistema de predicción emparentado con las tradicionales direcciones simbólicas. Puede apreciarse -o, al menos, esa es mi convicción- que, en general, los sucesos observados bajo la técnica de las direcciones armónicas encajan bastante mejor en el esquema de las casas intactas que en el de las casas iguales de la primera solución.
Esto de que las transformaciones armónicas sólo afectan al zodíaco se comprenderá mejor si consideramos una cuarta solución al problema de la representación gráfica de las cartas armónicas domificadas. Consiste en dibujar tantos zodiacos dentro de un mismo círculo como indique el número del armónico, pues esa precisamente era la idea original de Addey respecto de la naturaleza de los armónicos, tal como se muestra en la imagen siguiente:
Figura 5. John Addey. Armónico 2 con zodíaco duplicado
Vemos claramente en esta imagen cómo los planetas conservan sus emplazamientos originales en las casas y éstas mantienen también su estructura natural y su orden adecuado. Todo permanece en su lugar, excepto el lugar. El zodíaco se ha duplicado y esto nos permite entender inmediatamente por qué dos planetas en oposición en el armónico 1, están, sin embargo, en conjunción en el armónico 2. Obsérvese cómo Saturno y Urano, aun ocupando lugares opuestos del cielo (casas opuestas), quedan, sin embargo, referidos ambos al mismo signo del zodíaco. Esto es posible porque ahora tenemos dos zodíacos. También los teníamos antes, en los modelos anteriores del armónico 2, sólo que habian sido solapados, arrastrando consigo media carta cada uno y forzando un acoplamiento imposible. Ahora, sin embargo, vemos cómo el espacio ocupado inicialmente por el signo de Aries se lo reparten entre un nuevo signo de Aries de mitad de tamaño, pero del mismo número de grados, y otro nuevo de Tauro, de idénticas carácterísticas. Donde antes estaba Tauro, ahora están Géminis y Cáncer. En el lugar de Géminis, vemos a Leo y Virgo, etc. Con todo, esta cuarta solución está muy lejos de ser el modelo ideal. Intente representar de esta manera el armónico 60 de la misma carta y entenderá enseguida por qué tenemos que seguir buscando otra fórmula. Además, resulta muy difícil percibir los nuevos aspectos entre planetas armónicos en un modelo como éste (los aspectos dibujados aquí son, todavía, los del armónico 1, no los del 2), tanto más cuanto más elevado sea el armónico.
Aunque los armónicos se generan dividiendo en partes iguales el zodiaco original por cualquier número entero y haciendo encajar después en cada una de las partes un zodíaco completo en miniatura o a escala, hay una razón muy elemental por la cual las cartas armónicas se calculan multiplicando y no dividiendo. Si un planeta está, por ejemplo, a 20º de Aries en el armónico 1 ¿a dónde irá a parar en armónico 2? Puesto que el armónico 2 incrusta dos zodiacos de 360 grados cada uno en el mismo espacio donde antes había uno solo, resulta que ahora ese espacio aloja 720 grados; es decir, en cada sector ocupado originalmente por un grado, ahora caben 2. Y en los 20 grados que separaban al planeta en 20 de Aries del origen del zodiaco, ahora, lógicamente, caben 40. Por tanto, contando 40 grados desde el origen, resulta que el planeta estará ahora a 10 de Tauro. Y para pasar de 20 a 40 se multiplica por 2. Es de una sencillez sonrojante, pero lo que nos interesa realmente es otra cosa. Lo importante es que la fórmula matemática para el cálculo de los armónicos es igual de consistente con dos modelos teóricos muy diferentes.
Figura 6. Dos modelos de sucesión armónica
Si continuamos con el mismo ejemplo, nuestro planeta a 20 de Aries en el armónico 1 y a 10 de Tauro en el armónico 2, sumará otros 20 grados para alcanzar su posición en el armónico 3, y 20 más para cada uno de los armónicos que queramos añadir, siguiendo el orden natural de los números enteros. Esta progresión constante de 20 grados por armónico puede explicarse como el resultado de los sucesivos encogimientos del zodíaco hasta la mitad, un tercio, un cuarto, un quinto, etc, de su tamaño original, dependiendo del número del armónico. Hemos representado este modo de ver el asunto en la línea roja de la figura 6, adherida por ambos extremos a dos pequeños círculos marcados con un '1'. La línea roja atraviesa sucesivamente los zodíacos de los 12 primeros armónicos, cortándolos por posiciones que distan 20 grados entre sí, aunque, en realidad, están todas en el mismo lugar. Este modo de hablar es sumamente paradójico, pero caracteriza muy bien al primero de los dos modelos teóricos que hemos mencionado más arriba. Nos referiremos a él como modelo estático de las transformaciones armónicas. Este modelo estático concibe al planeta como fijo o inmóvil en una determinada posición, de modo que sus cambios a través de los armónicos no son realmente modificaciones de lugar, sino, simplemente dimensiones interiores presentes desde el principio en la posición original, aunque en forma replegada. Si, por decirlo así, desplegáramos a lo largo de un zodíaco natural único esas dimensiones replegadas en microzodíacos internos, nuestro planeta ocuparía simultáneamente todas las posiciones marcadas con los números del 1 al 12 en la figura 6. De hecho, son estas posiciones desplegadas de los planetas las que se representan gráficamente en las cartas armónicas convencionales. Por eso es que dos planetas en oposición natural aparecen dibujados juntos en la carta del armónico 2. Se trata, pues, de un recurso gráfico que no implica ningún desplazamiento real de ambos planetas hacia un lugar común, sino tan sólo una especie de desplazamiento virtual que expresa una propiedad matemática.
Supongamos ahora que nos tomamos al pie de la letra ese desplazamiento virtual, considerándolo como real. Esto implicaría que las distintas posiciones del planeta en los diferentes armónicos no son simultáneas, sino sucesivas. Ahora el planeta no permanece inmóvil, como hacía en el modelo estático, sino que avanza a saltos regulares girando incesantemente en un mismo zodíaco. Este nuevo modo de concebir las transformaciones armónicas es el modelo dinámico. El modelo estático concibe las transformaciones armónicas desde un punto de vista geométrico o espacial, mientras que para el modelo dinámico se trata de transformaciones de giro en secuencia temporal. Desde el punto de vista del modelo dinámico, la representación gráfica de una carta armónica no presenta problemas. Puesto que ahora lo que se altera es la posición del planeta en el zodíaco, pero no el zodíaco mismo, los signos y las casas deben permanecer en sus ubicaciones originales, tal como se mostraba en la figura 4. Ahora bien, sabemos que tanto en las direcciones simbólicas como en las direcciones armónicas mover las cúspides de las casas, de acuerdo con la misma norma por la cual son dirigidos los planetas da buenos resultados. Por consiguiente, la representación gráfica de una carta armónica más informativa y, a la vez, matemáticamente rigurosa, será la que combine en un mismo esquema los modelos mostrados en las figuras 3 y 4. Una posible forma de hacerlo se muestra en la figura 7.
Figura 7. John Addey. Armónico 2 con casas naturales y cúspides armónicas añadidas
Esta carta se diseña de acuerdo con la siguiente regla general: los sectores se conservan; los puntos giran en ellos. Los signos son sectores del zodíaco, las casas son sectores de la esfera local; unos y otros actúan como marcos o caminos. A través de ellos se desplaza todo lo que sea susceptible de localización puntual, es decir, los planetas, los nodos, los ángulos y las demás cúspides de las casas. Las cúspides tomadas aisladamente funcionan de manera semejante a las partes arábigas; condensan en un punto el significado de la casa y, mediante los aspectos de ese punto con los planetas, se forman nuevas posibilidades de interpretación.
El modelo de carta armónica de la figura 7 reúne en una sola rueda las virtudes de las tres soluciones posibles examinadas al principio, evitando, al mismo tiempo, todos sus inconvenientes. La única ventaja legítima del modelo de carta armónica con casas iguales es que sus (falsas) cúspides señalan los lugares que forman aspectos de la serie del 12 con el Ascendente armónico. Pero en el modelo de la figura 7, esos aspectos al Ascendente armónico están dibujados directamente; además, podemos dibujar también, si así lo deseamos, los aspectos al Medio Cielo armónico o a cualquier otro ángulo o cúspide armónicos. Por tanto, nada valioso se pierde aquí en relación con el primer modelo; además, nos libramos de las cúspides impostoras. La gran virtud del segundo modelo examinado es que es el único que nos da la posición correcta de las cúspides armónicas, pero éstas quedan como "flotando en el vacío", al perder la carta su orientación natural. Esta orientación se conserva en el tercer modelo, pero a costa de ignorar la posición de las cúspides armónicas. El modelo de la figura 7 mantiene en su parte interna la distribución original de las casas, situando, al mismo tiempo, en su parte externa las cúspides armónicas.
Parece que, felizmente, hemos hallado una solución satisfactoria al problema de la domificación de las cartas armónicas. Sin embargo, aún puede objetarse que esta solución está estrechamente vinculada con el modelo dinámico de las transformaciones armónicas, el cual, a primera vista, parece más endeble que el modelo estático. En principio, parece que el modelo estático explica mejor los rasgos de carácter permanentes que exhiben las personas con algún armónico fuertemente marcado; por ejemplo, el temperamento inquieto y tenso manifestado por aquellas personas cuyo armónico 8 presenta racimos de planetas agrupados en pocos grados, no es algo que sólo sea visible en el octavo año de su vida, sino que parece acompañarlas todo el tiempo. En general, todos los armónicos parecen estar permanentemente disponibles, lo que vale como prueba de que el modelo correcto es el estático. Se sobrentiende que las cartas armónicas no son otra cosa que dimensiones internas de la carta radical, siendo ésta fija e inmutable para toda la vida. Salir al paso de esta idea, que está como grabada a hierro candente en la mente de prácticamente todos los astrólogos, no se nos antoja tarea fácil. Y, sin embargo, no es más razonable suponer la inmutabilidad de la carta radical que sostener todavía, con Ptolomeo, que la Tierra está quieta en el centro del universo, o mantener, con Aristóteles, el fijismo de las especies. Lo cierto es que nada que esté vivo está inmóvil, y si una carta radical se manifiesta durante toda la vida, se debe precisamente a que la carta es algo vivo. Cómo puede estar en movimiento y, a la vez, presentar rasgos constantes no supone paradoja ni laberinto lógico alguno. Todo ser vivo mantiene su identidad gracias a la repetición cíclica de procesos metabólicos: el ritmo cardiaco, la respiración, la digestión, la alternancia de sueño y vigilia, el intercambio constante de materia y energía con el entorno. Del mismo modo, la carta radical puede representar un patrón de ciclos internos más bien que una imagen hierática del individuo.
Podemos tratar de conciliar ambos modelos sugiriendo que el modelo estático muestra todo lo que en una carta está en potencia, todo lo que puede llegar a ser en algún momento o repetirse cíclicamente cada cierto tiempo, mientras que el modelo dinámico señala la secuencia temporal y el ritmo en que estas potencialidades llegarán a manifestarse sucesivamente, por su resonancia con otros ciclos astronómicos o biológicos.
La eficacia de las direcciones armónicas y simbólicas en general como método de prognosis parece exigir la existencia de un radix dinámico, que vibra simultáneamente en multitud de longitudes de onda, a velocidades diferentes. Pero profundizar más en esta cuestión nos alejaría demasiado del propósito de este artículo, que no era otro que investigar la mejor manera posible de resolver el problema de la representación gráfica de las casas en las cartas armónicas. Hemos propuesto un modelo que consideramos superior a los que hasta ahora circulan y hemos sugerido algunas razones que pueden avalarlo teóricamente. Sólo nos resta invitar al lector a trabajar por algún tiempo con ese modelo, hasta que compruebe por sí mismo si le resulta o no útil o más informativo que los otros.
© 2007, Julián García Vara







Excelente articulo
ResponderEliminar