1. Qué es el vector armónico
El concepto de Vector Armónico fue introducido por Miguel García en varios de sus trabajos (1991, 1997) y nos remitimos a ellos para su formulación matemática precisa y su adecuada definición y cálculo.*
* Véase, por ejemplo, Una Formulación Matemática de los Harmogramas y de la Fuerza de los Números en las Cartas Astrales, en Suite Armónica, Ramses Ediciones, 1997, o Función de Onda Planetaria, Íbid.Sin embargo, para dar al menos una idea intuitiva, diremos aquí que el Vector Armónico de M.García está íntimamente relacionado con la Resultante Planetaria de A.Boudineau y que ésta, a su vez, puede considerarse como una respuesta al desafío de cómo calcular el punto medio de todos los planetas de una carta; más concretamente, es el producto de una suma de vectores, cada uno de los cuales representa la longitud eclíptica de un planeta en una carta astral determinada. Podemos imaginar la Resultante Planetaria como el lugar donde converge un conjunto de fuerzas cósmicas en conflicto, cada una de las cuales tira de la Tierra en una dirección diferente, pero todas con la misma intensidad. Señala, pues, el lugar del zodiaco donde se concentra toda la energía planetaria en un solo punto.
Podemos ver de modo gráfico cómo se efectúa esta suma de vectores valiéndonos del programa de cálculos astrológicos Armon**
** El programa Armon, cuyo autor es el propio Miguel García, es una maravillosa herramienta de trabajo e investigación astrológica que, aventajando en mucho a algunos de los mejores y más caros programas profesionales, ha sido declarado por su autor como de libre distribución. Pueden, pues, obtenerse copias gratuitas del mismo (por ejemplo, desde Escuela Venezolana de Astrología, donde se ofrece también un Manual de uso del programa Armon, de Elsa Rodríguez Vázquez y Mª Esperanza González Riesgo, que, en realidad, es mucho más que eso. Es un curso completo de técnicas astrológicas de prognosis). El programa Armon (del cual hemos tomado la mayor parte de los gráficos de este artículo) ofrece numerosas opciones que resuelven el cálculo del vector armónico y de la resultante planetaria. La que permite entender ésta última de forma más intuitiva es "Diseño de rueda 5,1,3/br,1". Conviene eliminar el dibujo de los aspectos (escogiendo la opción en blanco de "Modelo de aspectos") y limitar el número de planetas que se dibujan (en "Configurar" / "Planetas que se dibujan") y los que entran a formar parte del cálculo (en "Configurar" / "Dominios armónicos"). Una simple prueba con 3 ó 4 planetas es suficiente para comprender visualmente la sistemática del cálculo. Una vez entendida, pueden añadirse cuantos planetas se desee.
o bien echando un vistazo al esquema siguiente:
| Ejemplo de suma de vectores de tres planetas. | |
|---|---|
|
|
|
Paso 1. - Dibujamos el vector del primer planeta (Marte) |
Paso 2. - Dibujamos el vector del segundo planeta (Júpiter) |
|
|
|
Paso 3. - Transponemos el vector de uno de los planetas
|
Paso 4. - Trazamos la diagonal del paralelogramo resultante
|
|
|
|
Paso 5.- Dibujamos el vector del tercer planeta (Urano) |
Pasos 6 y 7. - Transponemos el vector del nuevo planeta
|
El vector que resulta del paso 7 es, naturalmente, el vector suma de los tres planetas; a éste puede sumarse, a su vez, el vector de un cuarto planeta, por el mismo procedimiento por el que se añadió un tercero a los dos primeros. Y al resultado de esto se le puede sumar un quinto vector, y así sucesivamente. El vector suma de todos los planetas es la Resultante Planetaria de Boudineau (RPB, de aquí en adelante). Este vector resultante apuntará a un grado del zodíaco, que es el que se puede considerar el punto medio de todos los planetas; pero, además de señalar ese importante punto de equilibrio o concentración de fuerzas, la suma de vectores proporciona información sobre la intensidad alcanzada por ese punto, la cual no es ni mucho menos la misma en todas las cartas. Esta intensidad está en proporción directa a la longitud del vector resultante.
El Vector Armónico de M.García extiende la aplicación de la RPB a todos los armónicos, entendidos éstos como ondas sinusoidales puras de amplitud 1 y frecuencia h (donde h es el número del armónico). Hasta aquí hemos explicado cómo se obtiene la RPB del armónico 1 de cualquier carta. Para obtener la RPB de otro armónico cualquiera, se calcula primero la carta de ese otro armónico y luego se procede igual que si se tratase del primer armónico.***
*** Estos cálculos constituyen la base de la Flor Armónica. Esta última es un recurso gráfico que representa simultáneamente la incidencia en el zodiaco de varios vectores armónicos correspondientes a las posiciones eclípticas de los planetas en las primeras 12 cartas armónicas, desplegados en tantos brazos (pétalos) equidistantes entre sí como sea el número del armónico. Para más detalles puede consultarse el artículo "Función de onda planetaria" , en op. cít. p.143 y ss.
Pero en este artículo nos vamos a limitar a trabajar con el armónico 1, lo cual facilitará mucho las cosas. Quizás esta restricción debiera conducirnos a abandonar la expresión "vector armónico" en favor de la RPB, pero la mantenemos por el tratamiento ondulatorio que se da a las representaciones gráficas asociadas al mismo, como pronto veremos.
2. Dificultades teóricas que entraña la noción de vector armónico.
Al margen de la complicación matemática de su cálculo, el vector armónico plantea dos problemas. El primero es a partir de qué planetas debemos calcularlo. El segundo, si está realmente justificado dar el mismo peso (matemático) a todos los planetas. En realidad, los dos problemas están íntimamente relacionados, pues si como respuesta al primero decidimos que hemos de dejar fuera, por ejemplo, los asteroides, Quirón y los planetas exteriores, incluyendo tan sólo los siete planetas tradicionales****,
**** Esta selección es la que viene "por defecto" en el programa Armón.
eso es tanto como admitir que no todo planeta merece la misma consideración ni, por consiguiente, el mismo peso en el cálculo. De esta manera, habríamos clasificado los planetas en dos grupos:
a) planetas de peso 1 (los 7 clásicos)
b) planetas de peso 0 (todos los demás)
Sin embargo, esta solución de tipo todo o nada parece demasiado drástica y tiene como resultado, entre otras cosas, equiparar la potencia de mercurio con la del sol. Después de todo, una selección como la que ilustramos parece no tener más fundamento que la costumbre, junto con vagas consideraciones acerca del tamaño, la distancia, la luminosidad y el estar esos planetas al alcance de la vista de unos ojos humanos sanos en condiciones de observación favorables.
La costumbre no constituye por sí misma ningún argumento de validez científica; en cuanto al tamaño, en términos absolutos urano y neptuno son mayores que mercurio, venus, marte o la luna;. y el sol es mucho mayor que todos los planetas juntos. Además, hay estrellas mucho mayores que el sol. En términos relativos (tamaño aparente en función de la distancia) el sol y la luna por sí solos deberían completar la selección. Si ponemos el énfasis en la distancia, forzoso sería incluir el cinturón de asteroides completo, además de los satélites de marte, júpiter o saturno. En cuanto a luminosidad, el sol barre de nuevo; además, habría que incluir las estrellas y los cometas y excluir a mercurio cuando no es visible. Y también habría que hacer esto último en relación al criterio de "perceptibilidad a simple vista". Como se ve por todo lo anterior, hacer una selección coherente de planetas no es tan sencillo; sin contar con la presumible intervención de todos los cuerpos celestes que todavía quedan por descubrir.
El segundo problema puede eludirse más fácilmente subrayando el carácter armónico del vector. Esto significa que no estamos tratando estrictamente con características materiales de los planetas, ni tampoco con la fuerza expresiva de los contenidos simbólicos que se les asocian. Tratamos nada más que con ángulos (que a su vez expresan ondas); y así como a la hora de calcular un punto medio entre dos planetas no les asignamos pesos relativos a cada uno, tampoco tenemos que hacerlo al buscar un punto matemático de equilibrio angular entre tres o más cuerpos.
Puede parecer un problema añadido que ciertas configuraciones planetarias (muy difíciles de hallar en la práctica, es verdad) dan como RPB un vector de longitud cero que no apunta a ninguna parte. Tal es el caso, por ejemplo, de un Gran Trígono (tres planetas, a intervalos de 120 grados) o de una Gran Cruz Cósmica (cuatro planetas a intervalos de 90 grados) y, en general, de cualquier distribución de n planetas que divida al zodíaco en n partes iguales. Pero esto no es un problema, sino una propiedad de la suma de vectores, ya que, en estos casos, la RPB apunta al centro de la carta. Esto, a su vez, significa que el armónico 1 (es decir, su onda asociada) es muy débil, pero, a cambio, el armónico n será sumamente poderoso. Y esto no escapa al vector armónico propiamente dicho, que recoge la suma de todos los armónicos.
Ante todas estas dificultades teóricas se puede reaccionar de muy diversas maneras. Quizás las tres salidas más típicas serían:
1) Efectuar una selección de planetas, ignorando todas las objeciones, al amparo del dicho "creo que esta es la selección correcta, porque lo siento así".
2) Darse por vencido y renunciar a trabajar con el vector armónico.
3) Ensayar distintas alternativas y observar su rendimiento para ver "cuál es la buena".
Pero cualquiera de estas soluciones parece viciada por la inclinación a creer que hay un vector armónico absoluto y sólo uno. Una solución más pragmática consiste en emplear la expresión vector armónico asociada en cada caso con una mención explícita de la selección efectuada. Nada nos impide hablar del "vector armónico de n planetas", en lugar de "vector armónico" a secas, siempre que especifiquemos la lista completa de planetas incluidos. Dicho de otra manera, si nadie ve un problema en el hecho de trabajar con el punto medio de sólo dos planetas, tampoco tiene por qué haberlo en usar algo así como el punto medio de, por ejemplo, sólo siete planetas. Ese punto que aglutina siete planetas debe ser interpretado -si es que alguien es capaz de hacerlo- como integrando los significados de todos y cada uno de esos siete planetas en relación al punto donde convergen. En cualquier caso, siempre indicará un punto sensible capaz de movilizar a todos los planetas implicados cuando sea activado por un tránsito o alguna otra forma de dirección.
Establecido esto, podemos pasar a mostrar alguna aplicación práctica de los vectores armónicos. Más concretamente, vamos a analizar qué puede aportar esta técnica al esclarecimiento de los condicionamientos astrológicos que pudieron intervenir en el maremoto que asoló Indonesia el pasado diciembre del 2004. No entraremos en grandes profundidades; en realidad, apenas si rozaremos lo estrictamente astrológico. De las tres preguntas que un estudio completo debiera tratar de responder -por qué sucedió eso, por qué sucedió entonces y por qué sucedió ahí- nos concentraremos tan sólo en la última, aunque también diremos algo de las otras dos. Pero para poder ensayar una respuesta a esta última, nos vemos precisados a combinar la técnica de los vectores armónicos con la astrocartografía.
3. Qué es la Astrocartografía.
Se suele decir que el zodiaco tropical tiene su punto de origen en uno de los dos lugares en que hacen intersección dos círculos máximos: el Ecuador Celeste y la Eclíptica. En realidad, ambos círculos son abstracciones geométricas, si bien podemos decir que hay un círculo natural que se corresponde muy aproximadamente con la eclíptica: el que describe el Sol a lo largo de un año sobre el telón de fondo de las estrellas fijas, visto desde la Tierra. El Ecuador Celeste tiene también un soporte natural, que no es otro que el Ecuador terrestre, del cual es una proyección.
4. Astrocartografía de vectores armónicos y tsunami del 2004.
De la misma manera que podemos ubicar un planeta sobre un mapa terrestre, podemos también localizar en ese mismo mapa el punto medio entre dos planetas. Y si podemos hacerlo con un punto medio, ninguna dificultad habrá en hacer lo mismo con un vector. De esta manera, el vector (RPB) señalará un lugar de la superficie terrestre que, al menos en teoría, recoge la máxima presión procedente de todos los planetas usados para el cálculo de ese vector.
El episodio del tsunami asiático de diciembre de 2004 ha cogido a la mayoría de los astrólogos con el pie cambiado. Casi nadie había previsto que pudiera suceder nada de una magnitud semejante en esas fechas. Unos pocos alzan sus voces para reivindicarse como excepciones a esta ceguera general. Sería injusto emitir un juicio genérico sobre todos ellos; como mínimo les asiste el beneficio de la duda. En cualquier caso, los plazos demasiado amplios y las descripciones demasiado genéricas no pueden computarse como aciertos. Por otra parte, como hay miles de astrólogos en el mundo, prediciendo constantemente todo tipo de cosas, es virtualmente imposible encontrar algún día que no esté incluido en la lista de fechas peligrosas de algún astrólogo. Entonces, cuando sucede algo impactante y mayoritariamente imprevisto, se arma un gran revuelo en torno al astrólogo que más se ha aproximado a una predicción correcta. Pero este mismo revuelo es sintomático. Significa que las técnicas más comúnmente utilizadas no permitían apreciar nada excepcional en relación con el momento y lugar del suceso. Significa también, en algunos casos, que había cundido una especie de -dadas las circunstancias- indecente nerviosismo profesional, al no tener nada que responder a quienes se les acercan preguntando qué extraordinarias señales había en el cielo acompañando toda esta conmoción en la Tierra. Y, más allá de la vanidad de cada cual, de hasta qué punto su imagen pública como astrólogo profesional sufra o no una cierta merma, está la desconfianza que en su propio interior puede surgir con respecto a la eficacia de los métodos que utiliza y hasta de la astrología como tal.
Sea cual sea el valor de la astrología en su estado actual y el grado de competencia adquirido por cada uno en el dominio de la misma, lo que es seguro es que no proporciona omnisciencia ni constituye un saber acabado al que no pueda incorporarse nada nuevo. Se impone, pues, el estudio, la investigación, la experimentación, la reflexión y el análisis de los hechos históricos, como única forma de ampliar perspectivas.
En un caso de maremoto, como el que nos viene ocupando, creo que, antes de aventurarse por el camino de las interpretaciones simbólicas con significado espiritual, conviene hacer un ensayo de análisis de bajo nivel, de astrología casi puramente física. Aquí es donde el vector armónico puede intervenir, entendido simplemente como un catalizador de fuerzas que presiona en una dirección. Esta dirección puede registrarse con las técnicas de la astrocartografía, y el programa Armon nos suministra para ello gráficos sumamente expresivos. Introduciremos los datos del suceso en los campos oportunos del programa y examinaremos, a continuación, uno de estos gráficos.
Tsunami: 26 diciembre 2004, 00h58m50s GMT,
epicentro: 3º 14' 24" N, 95º 49' 48" E
En el menú desplegable Graficos escogemos Diseño de página.
Se nos abrirá una ventana donde podemos escribir un texto que forme parte del nombre de una opción. Si la dejamos como está y pulsamos OK sin escribir nada, nos mostrará una larga lista de opciones, entre las cuales se encuentra Geo-Armonico Individual [w,a] (mapas), que es la que nos interesa. Si hemos hecho esto, sólo nos queda seleccionar esa opción con el ratón y aceptarla.
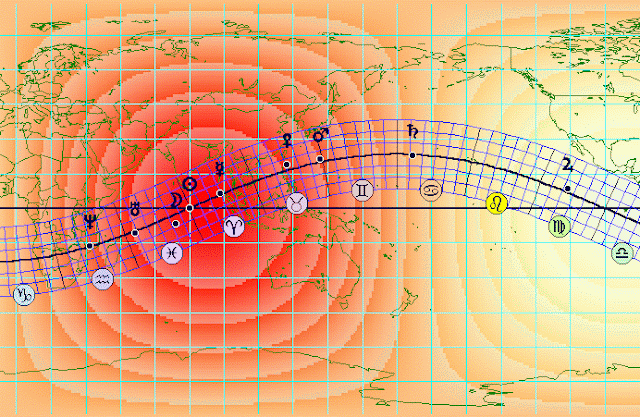
Pero podemos ganar tiempo escribiendo directamente "Geo-Armonico Individual [w,a] (mapas)" en la ventana de texto, ya sea la expresión completa o una parte de la misma. El programa tarda un poco en hacer los cálculos, pero, si todo va bien, finalmente veremos esto:
Inmediatamente llama la atención el grupo de ondas concéntricas de tonalidad rojiza que parecen propagarse en todas direcciones a partir de un punto próximo al epicentro del maremoto. De hecho, algunas personas sin conocimientos de astrología que han visto este gráfico han creído que se trataba simplemente de una representación pictórica de la onda expansiva del tsunami. Sin embargo, lo único que se representa aquí es la proyección astrocartográfica del vector armónico (RPB) del momento, que quedaría en el centro de los círculos rojos. Ese es el lugar de máxima intensidad, en torno al cual la tensión decrece paulatinamente.
No es fácil percibir los detalles geográficos ni los símbolos en una imagen del tamaño que muestra el programa. Para ver con más claridad a qué distancia del epicentro se sitúa el vector armónico es conveniente ampliarla.
Podemos hacerlo archivando la imagen como mapa de bits, mediante la opción Archivar Dibujo del menú Archivo. Una ventana de diálogo nos permitirá escoger la resolución deseada. Después, desde fuera del programa, podremos cargar la imagen con cualquier otro programa de procesamiento o visualización de imágenes. Por este procedimiento hemos generado, recortado y retocado el detalle ampliado de la imagen anterior. Ahora podemos ver que el vector armónico se encuentra a una distancia del epicentro que, traducida a tiempo, representa aproximadamente una hora. Es decir, que el vector armónico se demoraría aún una hora en llegar al epicentro, después de desencadenado el suceso. Y continuaría después girando en torno a la Tierra hasta completar una vuelta en unas 23 horas más. El vector armónico es, pues, un factor de desplazamiento rápido, demasiado rápido, diría yo, y apuntando a demasiados lugares en poco tiempo como para poder achacarle efectos tan desproporcionados. A lo sumo, podría actuar como el gorrión que se posa inocentemente en el tejado de una casa en ruinas, a punto de desplomarse, y le da el ligero empujón que la derriba definitivamente.
A pesar de lo impactante del gráfico, vemos enseguida que no hemos ido muy lejos. Además, hemos hablado del vector armónico sin precisar de qué vector armónico se trata. El vector armónico...¿de qué planetas? El programa lo indica en la parte superior de la ventana de gráficos, pero de una manera bastante críptica y en miniatura indiscernible. La misma información está accesible en el menú Configurar, opción Dominios Armónicos, donde podemos ver la secuencia de letras "elhvmjs". Cada letra representa un planeta, concretamente sol, luna, mercurio, venus, marte, júpiter y saturno. El programa calcula, por defecto, sólo en base a los siete planetas clásicos. Si en la misma opción de Dominios Armónicos añadimos "unp" a la serie de letras y, a continuación volvemos a calcular el gráfico, esta vez nos dará el vector armónico calculado a partir de urano, neptuno, plutón y los otros siete. ¿Qué sucede si hacemos esto? Pues que el vector armónico se desplaza a la derecha, quedando ahora bastante más lejos que antes del epicentro, como a tres horas y media de diferencia. ¿Podemos interpretar esto como un indicio de que los planetas exteriores cuentan poco y es preferible ignorarlos? No nos apresuremos. Pronto haremos una nueva prueba con ellos. Antes de eso vamos a investigar algo relacionado con la forma en que se desplazó de hecho la onda expansiva del maremoto a través de las aguas.
La cadena de olas llegó desde el epicentro hasta Somalia en unas seis horas, avanzando en dirección oeste a una velocidad que supera los 500 kilómetros por hora. El vector armónico de los siete planetas clásicos tardó una hora en alcanzar el epicentro y tan sólo media hora más en situarse justamente sobre la avanzada del tren de olas, en la misma dirección. Llegaría a Somalia entre una y dos horas antes que la montaña de agua. En cuanto al vector armónico de los diez planetas, partiría más rezagado y no daría alcance al frente de olas hasta las mismas costas de Somalia. En cualquier caso, estos vectores armónicos acompañaron de cerca el desplazamiento del fenómeno. Y esto constituye un dato más para que no podamos excluir del todo la relación entre los vectores armónicos y el acontecimiento estudiado.
Sin embargo, las conexiones siguen siendo muy débiles. El vector armónico barre todos los días tanto la zona siniestrada como el perímetro entero del planeta, en las proximidades del ecuador. Sería necesario disponer de alguna técnica que fijara el vector armónico en una zona bien determinada de la Tierra durante un periodo suficientemente amplio para que llegue a ser significativo en relación con cualquier cosa que en ese lugar pueda llegar a suceder. La astrología no nos deja sin recursos a este respecto. Nos brinda toda una serie de cartas que pueden cumplir esta función: las grandes conjunciones o configuraciones universales, los eclipses, las lunaciones y los ingresos del Sol en Aries figuran entre las más significativas. Aquí mostraremos tan sólo un ejemplo de aplicación de la técnica citada en último lugar. Las demás siguen un patrón similar. Sólo es necesario conocer con exactitud el día y la hora en que se ha de levantar cada una de esas cartas. El lugar para el cálculo del vector es irrelevante.
5. Cartas de Cero Aries y astrocartografía de vectores armónicos.
La técnica del Cero Aries es una de las más utilizadas en astrología mundial. Consiste en levantar una carta para el momento exacto en que el Sol ingresa en el signo de Aries. La domificación puede hacerse para cualquier lugar de la Tierra que nos interese estudiar. El periodo de vigencia de estas cartas es de un año, hasta el siguiente ingreso del Sol en Aries. Si deseamos saber cuáles serán las perspectivas generales del año para Madrid, sólo tenemos que calcular una carta para el día y hora GMT del ingreso del Sol en Aries, con las coordenadas geográficas de Madrid. O con las de Pekín, si queremos saber como se les presenta el año a los pekineses. Si no nos interesa ningún lugar en particular, sino tan solo las perspectivas del año en general, lo más lógico es calcular la carta para el lugar de la Tierra que deje al Sol en su cenit. Recordemos que el Cero de Aries tropical es el lugar de la esfera celeste donde se sitúa el Sol en el equinoccio de la primavera septentrional. Ese es, a su vez, uno de los puntos en que hace intersección el Ecuador Celeste con la Eclíptica. En la esfera terrestre, la intersección equivalente es la del ecuador terrestre con la eclíptica terrestre. Ese sería el lugar ocupado por el Sol en un mapa astrocartográfico y es, por consiguiente, el más indicado para levantar la carta de Cero Aries universal. Dado que, por definición, ese lugar ha de estar siempre en algún punto del ecuador, su latitud geográfica será siempre de 0º 0' 0". La longitud geográfica, sin embargo, cambiará de un año a otro. Los 4 ángulos de la carta coincidirán con las cúspides de los 4 signos cardinales y el MC coincidirá con el cenit.
Los datos necesarios para levantar la Carta de Cero Aries Universal o genérica del 2004 - 2005 son los siguientes:
20 de marzo del 2004 , 6h48m20s GMT
79º 46' 20" E , 0º 00' 00" N
Pasaremos por alto, sin embargo, la carta en sí, ya que aquí sólo nos interesa la astrocartografía del vector armónico. Utilizando los 10 planetas, obtenemos el siguiente resultado:
Como puede apreciarse, el vector armónico del año y el epicentro del tsunami ocupan ahora prácticamente el mismo lugar. La diferencia se puede estimar, a simple vista, como de unos 5 ó 6 grados de longitud geográfica, distancia que cabe holgadamente en el orbe de una conjunción. Si este gráfico fue diseñado para detectar el punto de la superficie terrestre más vulnerable en un momento decisivo, al aplicarlo junto a la técnica del Cero Aries nos debiera indicar una zona de alto riesgo en el periodo comprendido entre el 20 de marzo del 2004 y el 20 de marzo del 2005. A la luz de los hechos acaecidos, sobran los comentarios. El método obtiene un importante aval, aunque siga siendo cierto que una golondrina no hace verano. Por otra parte, si prescindimos de los planetas exteriores el ajuste no es tan preciso. El vector se desplaza unos 20 grados hacia el Este. En esta ocasión, los resultados son mejores usando 10 planetas que usando 7, lo que sugiere que los planetas exteriores son tan activos como los interiores. Puesto que usamos puntos medios simples que involucran a los planetas exteriores, no hay razón para excluirlos del cálculo de puntos medios complejos. Si esto es así, no podemos descartar que otros planetas aún no descubiertos merezcan un puesto en el cálculo de vectores. La imposibilidad de tenerlos en cuenta por el momento podría explicar las deficiencias observadas en el grado de precisión en el ajuste del vector.
© 2004, 2006, Julián García Vara












No hay comentarios:
Publicar un comentario