Direcciones Ecuatoriales de Arco Solar

Las Direcciones Ecuatoriales de Arco Solar que presentamos en este artículo constituyen un método de prognosis relativamente fácil de usar , en comparación con los principales sistemas de Direcciones Primarias tradicionales, entre los cuales cabría encuadrarlo. Aunque lo introducimos como una novedad, tiene un claro precedente, que es el Método de la Ascensión Recta de Sepharial. Explicaremos aquí ambos métodos, ilustrándolos con ejemplos. Pero antes de entrar en materia, haremos un repaso de algunos conceptos básicos relativos a la organización del espacio astronómico; sin ellos es imposible entender ninguna de las dos técnicas y aunque cualquier buen manual de astrología los contiene, es palpable que cada vez es mayor el número de estudiantes autodidactas de Astrología que creen poder saltar por encima de los fundamentos astronómicos de la misma, como si fueran competencia exclusiva de los programadores de software. Confiados en sus potentes programas de cálculos astronómicos, quedan confinados dentro de sus estrechos límites, sin poder hacer ningún progreso más allá de lo que éstos les ofrecen. Es más, ni siquiera entienden una parte considerable de las opciones incluidas en sus programas favoritos, y están, desde luego, enteramente incapacitados para detectar los errores de cálculo que casi siempre se deslizan, incluso en los mejores programas. Por el momento, ninguna de las dos técnicas de que aquí nos ocupamos está incluida entre las opciones de prognosis de los programas de cálculos astrológicos más difundidos; pero todavía puede sacarse partido de ellos si se comprenden las nociones básicas -muy elementales, por lo demás- acerca de coordenadas esféricas.


1. La organización del espacio astrológico. Conceptos básicos

La Eclíptica es el camino que aparentemente sigue el Sol, visto desde la Tierra, en relación al fondo de las estrellas fijas, de modo que completa un círculo al cabo de un año, cuyo centro es la propia Tierra. La medida de un radio de la Eclíptica se denomina Unidad Astronómica (UA) y se utiliza para medir las distancias que nos separan de los cuerpos celestes. Un círculo concéntrico al Ecuador terrestre y situado en su mismo plano, pero con un radio de 1 UA, se denomina Ecuador Celeste. El Ecuador Celeste es, por tanto, una proyección del Ecuador terrestre a la esfera celeste. La Eclíptica está inclinada unos 23º 27' en relación al Ecuador Celeste. Ambos círculos hacen intersección en dos puntos, que son precisamente los que cruza el Sol en los equinoccios. Uno de estos dos puntos, el ocupado por el Sol en el equinoccio de primavera septentrional, se toma como origen del zodíaco y de todas las mediciones que se refieren a cualquiera de ambos círculos. Se le conoce como Punto Vernal o Cero de Aries.

Figura 1

Aunque en realidad se trata en todo momento de proyecciones esféricas, la siguiente figura simplificada en términos de geometría plana ayudará a fijar estos conceptos y entender los que siguen. 

Figura 2

        En esta figura se representa un planeta que, como puede verse, no está situado en la Eclíptica, sino algunos grados al norte de la misma (en el punto P). Para fijar su posición en la Eclíptica, trazamos una perpendicular desde P hasta la Eclíptica; de este modo el planeta se proyecta en la Eclíptica exactamente en el punto C. La distancia desde el 0º de Aries hasta el punto C (segmento O-C), medida en grados, es la longitud eclíptica del planeta P. Así definida, se trata de la longitud eclíptica en grados absolutos. Pero generalmente se la suele expresar de manera abreviada en términos de signos del zodiaco y de grados contados desde el origen del signo de que se trate. Así, por ejemplo, un planeta cuya longitud eclíptica sea 135º estará a 15º de Leo, porque decir "15º de Leo" es lo mismo que decir "120º + 15º, desde 0º Aries". Es importante no perder de vista que lo que normalmente se representa en una carta astral como "planeta P" no es el punto P, sino el punto C. La distancia entre estos dos puntos (segmento C-P), medida en grados, es la latitud del planeta P. Esta latitud se llama Norte si el planeta queda al norte de la Eclíptica y, obviamente, se llama Sur si queda al sur. Puede darse el caso de que dos planetas que en la carta astral aparecen exactamente en la misma posición (por ejemplo, los dos a 14º23' de Sagitario), estén, sin embargo, alejados entre sí diez grados ó más. Tal sería el caso si la latitud de uno de ellos fuese, por ejemplo, 3º N, y la del otro 7º S. Por el contrario, si, además de la longitud, también la latitud fuese la misma, probablemente se daría un fenómeno de ocultación de un planeta por el otro, y la conjunción sería más potente y de consecuencias más drásticas. Si esos dos planetas son el Sol y la Luna, tendremos un eclipse de Sol. La eclíptica es, como su nombre indica, el lugar donde se producen los eclipses, ya que la Luna sólo puede ocultar al Sol si se sitúa a la altura de la eclíptica (latitud 0º). 

        Longitud y latitud se utilizan, pues, como un par de coordenadas cartesianas que permiten fijar la posición del punto P. Estos ejes de coordenadas son los más apropiados para seguir los movimientos de los planetas en sus propias órbitas. Son los que se suelen utilizar en todas las técnicas de prognosis de orientación zodiacal: tránsitos, progresiones secundarias, revoluciones solares, lunares y planetarias, direcciones de arco solar, direcciones simbólicas, direcciones armónicas, etc. 

        Otras técnicas de prognosis, como las diferentes variedades de direcciones primarias recurren a sistemas de coordenadas alternativos. Hay varios, pero el que aquí nos interesa es el de los ejes de coordenadas ecuatoriales. Ahora queremos proyectar el planeta P en el Ecuador Celeste y lo hacemos, como antes, trazando una perpendicular desde P hasta éste último. El punto A es la proyección de P en el Ecuador Celeste. La distancia desde el 0º de Aries hasta el punto A (segmento O-A), medida en grados, es la ascensión recta del planeta P. Al igual que sucede con la longitud, también la ascensión recta puede expresarse en términos de signos del zodíaco y grados de signos; pero en este caso es más frecuente expresarla en grados absolutos, porque el zodíaco remite de manera natural a la Eclíptica. También se suele expresar la ascensión recta en tiempo, lo cual facilita las observaciones astronómicas. En ese caso, se usan las siguientes equivalencias: 

• 1 hora de tiempo = 15 grados de arco (15º). 
• 4 minutos de tiempo = 1 grado de arco (1º).
• 1 minuto de tiempo = 15 minutos de arco (15').
• 4 segundos de tiempo = 1 minuto de arco (1').
• 1 segundo de tiempo = 15 segundos de arco (15").

       La razón de estas equivalencias es que expresan el tiempo que tarda la Tierra en efectuar una porción de giro sobre su propio eje igual a la medida del arco. La Ascensión Recta está, por tanto, directamente vinculada con el movimiento de rotación terrestre. 

        La distancia entre el punto A y el planeta P (segmento A-P), medida en grados, es la declinación del planeta P. Esta declinación se llama Norte si el planeta queda al norte del Ecuador y, nuevamente, se llama Sur si queda al sur. En astrología se da más importancia a las declinaciones que a las latitudes de los planetas. Esto se debe a que son utilizadas para definir un importante tipo de relación entre dos planetas: el aspecto de paralelo de declinación. Dos planetas están en paralelo (o paralela) de declinación si tienen la misma declinación, independientemente de cuál sea su longitud o su ascensión recta; el orbe máximo para este aspecto es de un grado. Para que haya un paralelo, la orientación tiene que ser también la misma, es decir, ambos planetas con declinación Norte, o bien ambos planetas con declinación Sur. El aspecto se juzga de manera similar a una conjunción. En caso de que la medida en grados de la declinación de dos planetas sea la misma, pero su orientación sea opuesta (es decir, uno al norte y otro al sur) se dice que están en contraparalelo de declinación y este aspecto se juzga de manera similar a una oposición. 

        La ascensión recta y la declinación cumplen en la esfera celeste la misma función que los meridianos y paralelos cumplen en el globo terráqueo. Dos planetas en paralelo de declinación mantienen entre sí la misma relación que dos ciudades cuya latitud geográfica sea la misma. Dos planetas con la misma ascensión recta mantienen entre sí la misma relación que dos ciudades cuya longitud geográfica sea la misma.   

Figura 3. Adaptada de un original de Michael Erlewine (1997) 

        Debido a la rotación de la Tierra, los planetas parecen moverse en círculos concéntricos que giran en torno a los polos. Éstos se denominan círculos de declinación y se corresponden con los paralelos del globo terráqueo. Dos planetas en aspecto de paralelo giran en el mismo círculo de declinación. Por tanto, el punto ocupado por uno cualquiera de ellos en el radix albergará al otro antes de que termine el día. Estas superposiciones de puntos son tan exactas como lo sea el paralelo, de modo que cuando un punto alcanza al otro se produce una situación semejante a la que provoca un eclipse. La diferencia, por supuesto, es que para entonces el otro planeta ya no está allí; pero eso mismo ocurre, por ejemplo, con los tránsitos.

        El hecho de que dos planetas en paralelo compartan el mismo círculo de declinación es lo que da a las declinaciones primacía sobre las latitudes; en principio, podrían tenerse en cuenta los "paralelos de latitud", pero éstos no llevan asociado ningún fenómeno astronómico comparable. El giro de planetas y estrellas en sus propios círculos de declinación, observable a simple vista, puede registrarse fotográficamente mediante cámaras fijas en trípodes que permiten exposiciones prolongadas; así se obtienen efectos como estos:

        Este sistema de coordenadas ecuatoriales es el más idóneo para registrar aquellos movimientos aparentes de los planetas que dependen directamente de la rotación de la Tierra sobre su propio eje. Éstos son precisamente los que interesan para trabajar con técnicas como el Método de la Ascensión Recta y las Direcciones Ecuatoriales de Arco Solar. Ahora estamos en mejores condiciones para abordarlas.

2. El método de la Ascensión Recta

        Charles E. O. Carter escribe en su Symbolic Directions:

podemos mover todos los planetas (o más bien, todas las posiciones radicales) en Ascensión Recta, un método fácil de direcciones primarias que fue publicado primero, según creo, por Sepharial en el British Journal of Astrology. Determinando la distancia en ascensión recta entre dos puntos cualesquiera que queramos dirigir, podemos convertir este "arco" en tiempo. Se han propuesto varias correspondencias, pero las dos principales son la de 1º de ascensión recta por año, y la de Naibod, el cual emplea el movimiento solar medio de 59' 8" al año. [Charles E.O. Carter, Symbolic Directions in Modern Astrology, p.18, Londres, 1947.]

        Prosigue Carter ilustrando el método con un ejemplo, en el cual, dejando a un lado algunas imprecisiones en los cálculos debidas a los limitados medios con que aún se trabajaba en su época, se aprecia que éste método no emplea directamente la ascensión recta de los planetas, sino la ascensión recta de su longitud eclíptica. Para que se entienda bien esta diferencia, la ilustramos de nuevo con una simplificación en geometría plana (figura 4).

Figura 4

        El punto C, como dijimos más arriba, es el lugar de la eclíptica en el cual se proyecta perpendicularmente el planeta P. Si ahora proyectamos el punto C perpendicularmente sobre el Ecuador Celeste, queda reflejado en el punto B. B define la ascensión recta de C, la cual es la medida en grados del segmento O-B. Es evidente que la ascensión recta del planeta P (es decir, O-A) no es la misma que la ascensión recta de la longitud del planeta P (es decir, O-B). La discrepancia entre ambas será tanto mayor cuanto mayor sea la latitud del planeta. En el caso de Plutón puede llegar a ser muy considerable. Y mucho más si trabajamos con estrellas fijas. 

        El método que Carter atribuye a Sepharial consiste, pues, en calcular una carta que registre la ascensión recta de las longitudes eclípticas de cada planeta (B en la figura 4); una vez hecho esto, para calcular una dirección de un planeta a un punto cualquiera de esa carta, se cuentan los grados desde el planeta hasta el punto y se hace valer cada grado por un año, o bien, preferentemente, cada 59'08" de arco (medida de Naibod) por un año. 

        Esto resultaba cómodo para ellos, ya que disponían de tablas para convertir fácilmente grados de longitud eclíptica en su ascensión recta correspondiente, como algunas publicadas por Alan Leo. Además, puesto que el Sol siempre está en la misma Eclíptica, su ascensión recta y la ascensión recta de su longitud es siempre la misma; esto permite saber cuál es la ascensión recta de un grado cualquiera del zodíaco mirando en las efemérides la ascensión recta del Sol cuando ocupa ese grado. Hay, además, una fórmula que permite convertir la longitud eclíptica en ascensión recta, y es la que Alan Leo daba en su libro de 1905 The Progressed Horoscope [Hay traducción española, en Edicomunicación S.A., Visión Libros, El Horóscopo Progresado, Barcelona, 1988.], en los términos siguientes: 

FORMULA I Para convertir la Longitud en Ascensión Recta, sin la Latitud.
    Log. coseno de oblicuidad de la eclíptica (23º 27')
+ Log. tangente long. desde ARIES o LIBRA (o Log. cotan. long. desde CANCER o CAPRICORNIO)
= Log. tangente A.R. desde ARIES o LIBRA (o Log. cotan. A.R. desde CANCER o CAPRICORNIO)
    Si en ARIES, TAURO o GEMINIS, la solución será la A.R. que se necesita. Si en CANCER, LEO o VIRGO, añadir 90º. Si en LIBRA, ESCORPIO o SAGITARIO, añadir 180º. Si en CAPRICORNIO, ACUARIO o PISCIS, añadir 270º.
    NOTA: Esta fórmula se emplea en el caso del Sol o cualquier cuerpo celeste que se toma sin la latitud o de cualquier grado de la eclíptica sin latitud. 

       Sin embargo, esta fórmula resulta inútil si no se dispone de las tablas de logaritmos. Afortunadamente una calculadora científica nos exime hoy de ellas, pudiendo emplear en su lugar la siguiente variante: 

Para puntos situados en ARIES, TAURO o GEMINIS, medidos desde 0 de ARIES, o bien en LIBRA, ESCORPIO o SAGITARIO, medidos desde 0 de LIBRA: atan (( cos (OE)) x tan (long))	Para puntos situados en CANCER, LEO o VIRGO, medidos desde 0 de CANCER, o bien en CAPRICORNIO, ACUARIO o PISCIS, medidos desde 0 de CAPRICORNIO: atan (1/( cos (OE) x 1/tan (long)))
( siendo "OE" la Oblicuidad de la Eclíptica y "long" la Longitud Eclíptica)
Si en ARIES, TAURO o GEMINIS, la solución será la A.R. que se necesita. Si en CANCER, LEO o VIRGO, añadir 90º. Si en LIBRA, ESCORPIO o SAGITARIO, añadir 180º. Si en CAPRICORNIO, ACUARIO o PISCIS, añadir 270º.

      Si dispone de Microsoft Excel todo lo que necesita es la siguiente:

Hoja de cálculo para convertir la Longitud en Ascensión Recta sin Latitud

Por si todavía quedase alguna duda, incluiremos el ejemplo que da el propio Carter, valiéndose de la carta siguiente: 

Figura 5

       La de arriba -explica Carter, p.19 y ss.- es la natividad de un hombre, nacido en Wiltshire a las 8.10 a.m., 25 de junio de 1891. El 30 de octubre de 1923 fue contratado para supervisar una correa de impulsión en una fábrica donde él trabajaba como ingeniero. Ordenó a un operador que detuviera la maquinaria, pero éste último, por equivocación, la activó de nuevo. El nativo sufrió el desgarro de su brazo, sepsis permanente y su vida fue salvada por poco. Fue compensado por su firma, pero su carrera estaba arruinada. (...) 

Tomemos la Luna en oposición a Marte. 

       A.R. 14º 48' Acuario = 317º 16' 

       A.R. 14º 13' Capricornio = 285º 26' 

_______________________________________________ 

       Diferencia = 31º 50' 

Sumar, para ecuación de Naibod, 29' * 

[* El propio Carter explica esto así: "La medida de 59' 8" no es tan difícil de usar como podría suponerse. Es, por supuesto, más lenta que la de 1º, y por tanto indica una fecha posterior en la vida. Para convertir el arco de 1º en el de Naibod, súmese al primero tantos minutos como grados haya (redondeando el arco al grado más cercano, de modo que, v.g. 20º 50' se redondea a 21º) menos tantos minutos como decenas de grados haya, de nuevo redondeando a la decena más cercana. Por tanto 20º 50' sería más 21' menos 2'. El resultado quedará siempre lo suficientemente cerca para todos los propósitos ordinarios. 

Damos esta información por su interés histórico, para situar la cita en su adecuado contexto; pero, obviamente, estos procedimientos sobran hoy en día. Si se dispone de una simple calculadora científica con funciones trigonométricas, basta con dividir el arco de dirección entre 0º 59' 8" ó 0.98555 para obtener directamente el resultado buscado y con mayor precisión. ] 

________________________________________________ 

               = 32º 19' 

       Esto queda muy cerca del tiempo del accidente, el cual ocurrió a la edad de 32 años y 127 días; 127 días son en relación a un año de 365 días, como 21' es a 60', de modo que la edad de 32 años, 127 días la expresaremos como 32º 21', en términos de arco. 

       (...) la Luna, llevada a través del cielo a razón de 59' 8" por año, alcanzaría la oposición al lugar radical de Marte en 32 años y 19/60 de año. Ahora bien, el accidente ocurrió a la edad de 32 años y 21/60, o un trigésimo de año más tarde. En otras palabras, la dirección se cumple alrededor de 12 días después, una discrepancia relativamente muy pequeña. 

        Se observará también por este ejemplo que la Luna es dirigida hacia la oposición de Marte en dirección contraria a su movimiento natural en el zodíaco, puesto que se la desplaza desde Acuario hasta Capricornio. Así se hace siempre por este método. La razón de ello es que está basado en el movimiento de rotación de la Tierra, que es el que hace aparecer a los planetas por el horizonte oriental y ocultarse por el occidental en dirección contraria a su avance en el zodiaco.


3. Las direcciones ecuatoriales de arco solar

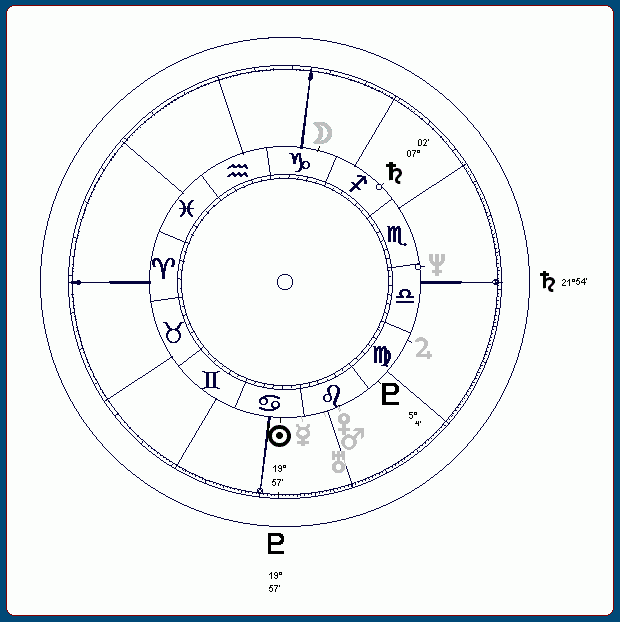
       La carta astral que se muestra a continuación corresponde a un hombre nacido el 11 de julio de 1957, a las 1:05 horas CET, en Málaga, España, 36º 43' N, 4º 25' W. Se suicidó el día 10 de agosto del 2004, de manera ritual, ahorcándose en medio de numerosas velas encendidas, poco después de cumplir los 47 años. 

Figura 6

        Una dirección concordante con el suceso podría ser Plutón en conjunción al Sol. Plutón comparte con el signo de Escorpio un fondo pulsional que, mal enfocado, puede generar tendencias autodestructivas. Además, en esta carta la cúspide de la casa octava (tradicionalmente asociada a la muerte) se encuentra en el signo de Escorpio. De acuerdo con la versión moderna más utilizada de la teoría de las dignidades planetarias (de la que no me siento muy convencido, aunque tampoco la rechazo por principio) Plutón sería aquí el regente de la casa VIII y, por estar en Leo, el Sol es su dispositor. Todo esto (o simplemente la presencia de Plutón en Leo) puede incorporar a las tendencias autodestructivas matices exhibicionistas e histriónicos. Una dirección Plutón-Sol, por otra parte, admite por sí sola esa lectura, aun en ausencia de los otros antecedentes. Además, la medida del ángulo Sol-Plutón en grados no anda muy lejos de la edad del sujeto, y menos aún en Ascensión Recta, por lo cual merece la pena ensayar la aplicación del método anterior a este caso. 

• El Sol se encuentra a 18º 25' 36" de Cáncer. La ascensión recta del Sol es 109º 57' 31", tanto del planeta como de su longitud.
• La ascensión recta de la longitud de Plutón (28º 48' 27" de Leo) con una oblicuidad de la eclíptica de 23º 26' 41" es igual a 150º 56' 58".
• La diferencia de ambas ascensiones rectas nos da el arco de dirección = 40º 59' 27".
• Corrección de Naibod = 41º 35' 19".
• Edad en arco = 47º 05' 02".

El error es de 5 años y medio, lo cual obviamente es demasiado. Parece que esta dirección no tuvo mucho que ver con el suceso. Y sin embargo, si observamos lo que se ve en la figura 7, resulta difícil aceptar que así sea.

 Figura 7

        La figura 7 es una representación esférica de la misma carta astral de la figura 6. Para mayor claridad, se han omitido todos los planetas, excepto los que incumben a la dirección investigada. Hemos escogido coordenadas ecuatoriales, porque son las idóneas para el método de la Ascensión Recta. La ventaja de usar este tipo de carta tridimensional es que nos permite darnos cuenta enseguida de que el Sol y Plutón tienen un importante vínculo: un paralelo de declinación exacto al minuto de arco (22º 11' Norte, en ambos planetas). Se mueven por tanto exactamente en el mismo círculo de declinación, de modo que cuando uno de ellos alcance la posición del otro por dirección, se producirá un fenómeno análogo a la ocultación de un planeta por el otro. Esta no es, por tanto, una dirección más, sino que es de esperar que sus efectos queden sobredimensionados. 

        En segundo lugar, observamos que el ángulo entre el Sol y Plutón, medido en ascensión recta de los planetas mismos (en lugar de la ascensión recta de sus longitudes) asciende a 45º 06'. Si tomamos esta medida como arco direccional y aplicamos la corrección de Naibod, llegamos a 45º 46'. Esto nos deja a un año y cuatro meses de la fecha del suceso. Este resultado no es tan malo como el anterior, ya que hemos recortado en más de cuatro años la diferencia, pero aún dista de ser convincente.

        La medida de Naibod, según dejamos dicho, es la media del movimiento diario del Sol. Si el Sol recorre los 360º del Zodíaco en un año trópico, y éste consta de 365,2421991 días, entonces en promedio el Sol recorre 360/365,2421991 grados por día, es decir 0º 58' 08.33". Hay otra técnica de prognosis más conocida que la que aquí estamos tratando que también utiliza el movimiento diario del Sol como clave de dirección para todos los planetas. Se trata de las llamadas Direcciones de Arco Solar. Es muy semejante al método de la Ascensión Recta, excepto en tres detalles:

• No usa la ascensión recta de las longitudes de los planetas, sino las longitudes eclípticas mismas.
• No mueve los planetas en sentido horario, sino en sentido zodiacal.
• No usa el movimiento diario medio del Sol (la medida de Naibod) sino el movimiento diario real del Sol.

       Esta última diferencia es la que nos interesa ahora. El Sol no se mueve todo el tiempo a la misma velocidad en el zodiaco. Esto se debe a que la órbita de la Tierra no es un círculo perfecto, sino una elipse. Cuando el Sol se sitúa cerca del perihelio, actualmente en Capricornio, su movimiento es más rápido; cuando se mueve en las inmediaciones del afelio, actualmente en Cáncer, lo hace más lentamente. La idea clave que está detrás tanto del método de la Ascensión Recta como de las Direcciones de Arco Solar es: 

        Lo que el Sol se mueve en un día, eso se mueven todos los planetas en un año 

        Es decir, cada día contado a partir del nacimiento vale por un año contado a partir del mismo origen. El método de la Ascensión Recta simplifica los cálculos tomando el valor medio del movimiento diario solar como clave de velocidad constante. Las direcciones de Arco Solar optan por el desplazamiento verdadero del Sol, diferente en cada natividad, y de velocidad variable para las distintas edades. 

        Veamos qué sucede si en nuestro cálculo anterior, en el cual ya habíamos sustituido la ascensión recta de las longitudes de los planetas por su verdadera ascensión recta, sustituimos ahora también el movimiento medio del Sol (Clave de Naibod) por su movimiento verdadero. 

• La edad del nativo en cuestión para la fecha del suceso era de 47 años y 30 días (47º 05'02" en arco ó 47.083826 años)
• Tomando cada año por un día, esto equivale a 47 días 2 horas 0 minutos 43 segundos.
• Sumando esos días a la fecha de nacimiento, llegamos al 27 de agosto de 1957, 2h 05m 43s GMT.
• En esa fecha y hora el Sol se encuentra en Virgo, a 3º 32' 16".
• Desde la posición natal del Sol (18º 25' 36" de Cáncer) hasta 3º 32' 16 de Virgo hay un arco de 45º 06' 40" (el Arco Solar verdadero). Esto es lo que debemos restar a la ascensión recta de Plutón.
• La ascensión recta de Plutón es 155º 03' 49" - 45º 06' 40" = 109º 57' 09".
• La ascensión recta del Sol es 109º 57' 31".
• Diferencia = 0º 00' 22".

       Ahora el arco de dirección sólo ha sido rebasado por el arco solar en 22", lo que traducido a tiempo de cumplimiento nos arroja un error de poco más de 2 días (cada día equivale aproximadamente a 10" de arco)**

** Todos los cálculos anteriores se pueden abreviar bastante si se dispone de programas de cálculos astrológicos. Para trabajar con el método que acabamos de descubrir podemos usar cualquier programa que ofrezca el listado de la ascensión recta de los planetas. Casi todos lo hacen y algunos incluso permiten dibujar la carta astral completa en coordenadas ecuatoriales. Así, por ejemplo, el Astrolog y el Zet. De ese modo, determinamos el arco de dirección con una simple resta. El arco solar puede obtenerse directamente de las Progresiones Secundarias o de las Direcciones de Arco Solar, ya que es el mismo en ambos métodos

       Que sepamos, la hora de nacimiento no había sido rectificada, por lo que un error de unos pocos minutos podría ajustar todavía más esta dirección hasta dar en el día exacto. En realidad, basta con retroceder dos minutos la hora de nacimiento para que una segunda dirección, tan peligrosa como la anterior, se cumpla exactamente en la fecha del suceso, por el mismo sistema que estamos considerando. El ascendente, que en longitud eclíptica está a 24º 25' de Aries, medido en ascensión recta queda a 22º 37' del mismo signo. Dos minutos antes estaba a 21º 45' de Aries. La ascensión recta de Saturno dirigida por arco solar queda a 21º 45' de Libra, en lo que sería una oposición exacta a ese supuesto ascendente. 

Figura 8

        Pero no queremos recurrir a hipótesis ad hoc. Más bien debemos considerar que este resultado es más que satisfactorio, sobre todo teniendo en cuenta que uno de los planetas involucrados en la primera dirección es el Sol y que a éste se le conceden orbes mayores. A diferencia de los otros planetas, cuya ubicación es más puntual, el disco del Sol visto desde la Tierra tiene un diámetro de 31' de arco. Por tanto, una dirección al Sol entra en contacto con éste ya desde 15' de arco antes de la posición registrada en las efemérides y se prolonga por otros 15' más; esto significa que por un espacio de seis meses (tres antes y tres después de la fecha calculada) la dirección puede considerarse como muy activa por todo ese tiempo. Podemos resumir el caso como sigue: 

• Hallamos al Sol y a Plutón en paralelo de declinación exacto al minuto (22º 11' N)
• El arco de dirección Plutón-Sol, en ascensión recta, es de 45º 06'
• Se produce un suceso concordante con la dirección Plutón-Sol a la edad de 47,084 años
• A los 47,084 días después del nacimiento, el arco solar asciende a 45º 06'

        Nos faltó calcular la dirección Sol-Plutón por Direcciones (eclípticas) de Arco Solar. Sin entrar en más detalles, ya que no es el tema de este artículo, diremos que por ese método se produce de nuevo un desfase en torno a los cinco años.

        Hemos asistido, por consiguiente, a la evolución desde el "método de la Ascensión Recta" a las "Direcciones Ecuatoriales de Arco Solar", pasando por las tradicionales "Direcciones de Arco Solar" (eclípticas). Estas denominaciones, desde luego, son discutibles, pero de algún modo hay que referirse a estos procedimientos. Tan método de ascensión recta es el primero como el segundo y, a decir verdad, incluso le cuadra mejor el título al segundo que al primero. Y ambas son desde luego direcciones ecuatoriales, una de arco solar medio y la otra de arco solar verdadero. Por tanto las tres son direcciones de arco solar, si bien el método de la ascensión recta lo es sólo en parte, ya que admite otras claves (1º por año, por ejemplo). No obstante, dado que las técnicas ya en uso son conocidas por esos nombres, no vamos a disputárselos. Resumimos en el cuadro siguiente las características de las tres:

	Método de la Ascensión Recta	Direcciones de Arco Solar	Direcciones Ecuatoriales de Arco Solar
Los arcos de dirección se miden	En ascensión recta de las longitudes eclípticas	En longitudes eclípticas	En ascensión recta (de los planetas mismos)
Clave de dirección por año	a) Medida de Naibod  (0º 59' 08.33") b) Un grado.	Arco solar diario verdadero (eclíptico)	Arco solar diario verdadero (eclíptico)
Los planetas son dirigidos en sentido	horario	zodiacal	horario

4. Arco solar y resonancia de ciclos

        La referencia de los tres métodos anteriores al arco solar, ya sea medio o verdadero, se debe a que la tradición astrológica nos ha legado el hallazgo de que un día equivale simbólicamente a un año y se proyecta o refleja en él; de ahí que en las técnicas que acabamos de describir el movimiento eclíptico (medio o verdadero) del Sol en un día se tome como pauta del movimiento de toda la carta (ecuatorial o eclíptica) en un año. Esta equivalencia, sin embargo, es indirecta y hasta se diría un tanto rebuscada si no fuera porque en la práctica produce buenos resultados.

        Detrás de la idea que acabamos de exponer está el supuesto de que dos ciclos diferentes pueden afectarse mutuamente por un fenómeno de resonancia, de apariencia ondulatoria. De todos los ciclos que estudia la astrología hay dos que nos afectan de manera muy fundamental, por el simple hecho de habitar el planeta Tierra; son precisamente los que se derivan de los dos movimientos principales de nuestro planeta: el de rotación en torno a su eje y el de revolución en torno al Sol, es decir, el día y el año. Las tres técnicas que hemos explorado, junto con las progresiones secundarias y las direcciones primarias, son distintos intentos de poner a prueba el alcance de esta postulada resonancia de ciclos y de sacarle partido para propósitos de prognosis astrológica. Cada una lo hace "a su manera".

        Hemos transformado el método de la Ascensión Recta de Sepharial en las Direcciones Ecuatoriales de Arco Solar sustituyendo dos medidas matemáticas abstractas por otras dos más estrictamente astronómicas. Además, hemos incorporado los paralelos de declinación a la técnica, como forma de seleccionar las direcciones más relevantes. Con esto no pretendemos haber superado el sistema de Sepharial, sino solamente haberlo completado con una interesante variante. Las longitudes eclípticas de los planetas han demostrado su utilidad en buena parte de las herramientas de trabajo astrológico, por lo que no es de extrañar que tambiém sus ascensiones rectas tengan importancia y puedan protagonizar direcciones. Carter defiende el método de Sepharial con estas palabras:

pienso que este método tiene mucho valor [en mi experiencia se acerca extraordinariamente en el tiempo, quedando a menudo a muy pocos días de la fecha exacta] y es mucho más simple que las primarias convencionales. 

       Esto puede deberse al valor intrínseco del método, pero debemos observar que para fechas natales más próximas a los equinoccios que a los solsticios, la medida de Naibod y el Arco Solar difieren muy poco. Además, para planetas con poca latitud, no hay tampoco mucha diferencia entre la ascensión recta del planeta y la de su longitud eclíptica; por tanto, algunas direcciones funcionarán bien aunque el método no sea bueno, al beneficiarse de su accidental aproximación a otro método mejor. Claro está que el beneficiado podría ser cualquiera de los dos. Sólo quiero llamar la atención sobre el hecho de que si sólo uno de ellos fuese eficaz, aún podrían obtenerse de vez en cuando buenos resultados con el otro, y esto dejando completamente a un lado el porcentaje de aciertos debidos al azar.

        Prosigue Carter, comentando el método de la Ascensión Recta:

Pero no es simbólico (...) porque hay un movimiento uniforme real de todas las posiciones radicales, debido a la rotación de la tierra, el cual es semejante para todos, ya se trate del lugar radical del lento neptuno o de la rápida luna. Cada uno cruza el cielo de este a oeste sobre el horizonte, y de oeste a este por debajo del horizonte, en arcos paralelos al ecuador celeste y entre sí, así que cada punto llega, en un momento u otro, a la misma distancia, en ascensión recta, desde el meridiano que cada uno de los otros puntos ocupaba en el nacimiento. 

        Este es uno de los dos extremos de la base astronómica de la técnica: los movimientos aparentes diarios de los planetas (o de sus grados de longitud) en sus respectivos círculos de declinación, medidos en ascensión recta. El otro extremo es el movimiento anual del Sol en su propia órbita aparente (la eclíptica), medido en longitud. Pero si lo observamos con detenimiento, estas técnicas parecen dar un salto en el vacío en su peculiar modo de aplicar la ecuación día-año. Consideremos el ejemplo mostrado en las figuras 6 y 7. El arco de dirección Plutón-Sol, de 45º 06' 18" en A.R., puede expresarse en tiempo como 3 horas 0 minutos 25 segundos; este es el tiempo real que emplea Plutón en alcanzar la posición radical del Sol durante las primeras horas de la vida del nativo. Por tanto, esta dirección se cumple primero como tránsito ecuatorial en la tercera hora de la vida. Este tiempo representa el 12,53% de un día. Si decimos que un día equivale a un año, entonces el 12,53% de un día equivaldrá al 12,53% de un año. El 12,53% de un año son 45,76 días (esto en promedio, es decir, usando la medida de Naibod). Por tanto, la dirección Plutón-Sol se cumple por segunda vez a los 45,76 días de vida (o a los 47,08, usando arco solar). Esta es realmente la primera proyección que cumple directamente la ecuación día-año. Ahora bien, puesto que la dirección Plutón-Sol se refleja a los 45,76 días de vida (ó 47,08), siendo un día = un año, puede reflejarse en segunda instancia a los 45,76 años (ó 47,08) de edad.

Figura 9

        Se trata pues de proyecciones de proyecciones; el segundo término de la comparación está elevado al cuadrado. La base realmente empleada aquí como resonancia de ciclo es:

        1 día = (365,24)² días

        Algo semejante sucede con las direcciones primarias convencionales. Aunque distintos autores utilizan diferentes claves de dirección, todas ellas se hallan próximas a una fracción de día que es al día entero lo que éste es a un año. Y esa fracción de día es equiparada directamente con un año. Por el contrario, las progresiones secundarias no elevan el segundo término al cuadrado, sino que respetan el sentido original de la ecuación día-año; toman nota de los movimientos planetarios registrados en la eclíptica durante los primeros días de la vida y los proyectan proporcionalmente en los años equivalentes. Desde el punto de vista del nivel de proyección, las progresiones secundarias son realmente primarias; y las direcciones primarias son secundarias o derivadas.

        Una cuestión interesante suscitada por estas técnicas es si esta acumulación de proyecciones disminuye o, por el contrario, aumenta la eficacia de la dirección. No tengo respuesta para ello, pero al menos puedo ensayar una reflexión. Una misma película puede proyectarse en una pantalla tan pequeña como la de un teléfono móvil o tan grande como la de una importante sala de estreno. Es posible que a medida que el tamaño de la pantalla aumenta, la definición disminuya; pero, a pesar de ello, su impacto visual es considerablemente mayor. Análogamente, una dirección que dura un espacio muy breve de tiempo puede ser muy nítida por un instante, pero apenas tendrá tiempo de causarnos ninguna inquietud. Al proyectarla sobre un ciclo más amplio, se hace considerablemente más lenta y persistente, de modo que el ciclo resonante mayor funciona como un amplificador de la onda original.

        Para terminar indicaré que, a mi modo de ver, de todas estas técnicas la que hace una lectura más pura de la ecuación día-año es la que he denominado Direcciones Ecuatoriales de Arco Solar. El ciclo que determina la naturaleza y duración de un día es el movimiento de rotación terrestre, y éste es el que origina los movimientos aparentes de los planetas en sus círculos de declinación; para determinar estos movimientos, es necesario tener en cuenta la ascensión recta de los planetas mismos (no la de sus longitudes). El ciclo que determina la naturaleza, desarrollo y duración de un año es la revolución de la tierra en torno al sol, y esta es la que origina el movimiento aparente del sol en la eclíptica. Por tanto, un arco de ascensión recta debe corresponderse con un arco igual de desplazamiento del sol en la eclíptica. Bien es verdad que la aplicación literal de lo que acabo de decir nos conduce a la proyección en primera instancia que suele cumplirse en las primeras semanas o meses de la vida, mientras que el método de las Direcciones Ecuatoriales de Arco Solar no toma éstas en cuenta, sino sólo la proyección en segunda instancia. En compensación, pueden observarse efectos elevados al cuadrado.

© 2007, Julián García Vara